KABARPANDEGLANG.COM – Lingkaran merupakan kumpulan titik-titik pada bidang datar yang jaraknya sama terhadap suatu titik tertentu. Hal-hal yang berkaitan dengan bulat yaitu jari-jari, busur, tali busur, diameter, apotema, keliling dan sebagainya. Pada tulisan ini hanya akan membahas mengenai keliling bundar saja.
Keliling (K) merupakan busur terpanjang pada lingkaran.Keliling bulat berkaitan dengan salah satu konstanta matematika yang paling penting. Konstanta ini, yaitu pi. Phi telah dikenal selama hampir 4.000 tahun. Huruf π yakni abjad Yunani yang dibaca pi dan phi juga mampu dipakai dalam penulisan. Perhatikan penjelasan berikut ini.
Beni menggambar lingkaran menggunakan jangka pada kertas karton dengan jari-jari 7 cm. Beni mengukur keliling bulat. Hasilnya 44 cm. Beni membandingkan antara panjang keliling dengan panjang diameter. K adalah panjang keliling bundar dan d adalah panjang diameter lingkaran. Perbandingan antara keliling dengan diameter yakni sebagai berikut.
| K | = | 44 | = | 22 |
|---|---|---|---|---|
| d | 14 | 7 |
Beni menggambar bundar memakai jangka. Beni menggambar di kertas karton dengan jari-jari 5 cm. Beni mengukur keliling bundar. Hasilnya 15,7 cm. Beni membandingkan antara keliling dengan diameter, adalah
| K | = | 15,7 | = 3,14 |
|---|---|---|---|
| d | 5 |
Berdasarkan acara di atas, maka nilai K/d disebut konstanta π (π dibaca phi). Kaprikornus, nilai pendekatan untuk π yaitu 22/7 atau 3,14. Berdasarkan Pengamatan tersebut, maka mampu disimpulkan bahwa :
| π = | K |
|---|---|
| d |
Untuk mencari panjang keliling bundar bila diketahui diameter ialah dengan rumus sebagai berikut
K = π x d atau K = π d.
Diameter besarnya sama dengan dua kali jari-jari (d = 2r). Jika bulat diketahui jari-jarinya maka
K = π x 2 r atau K = 2πr
Contoh Soal 1
Sebuah bundar mempunyai jari-jari 14 cm. Berapakah keliling bulat tersebut?
Penyelesaian
K = 2 π r
| K = 2 x | 22 | x 14 |
| 7 |
K = 2 x 22 x 2
K = 88
Makara, keliling lingkarannya yakni 88 cm.
Contoh Soal 2
Dayu ingin menghias keliling tutup kawasan masakan. Dayu menghiasnya dengan pita berwarna biru. Dayu perlu memilih panjang diameter tutup terlebih dahulu.
Cara mengukur garis pada tutup masakan Dayu. Dayu menerima panjang garisnya yakni 15 cm. Berapa cm panjang pita yang diharapkan Dayu yang sempurna?
Penyelesaian
Rumus keliling bulat yaitu K = π d.
Kemudian, masukkan nilai π = 3,14 dan d = 15 cm.
Dengan demikian, diperoleh
K = 3,14 x 15
K = 47,1
Jadi, panjang pita yang diharapkan Dayu yaitu 47,1 cm.
Ayo Mencoba
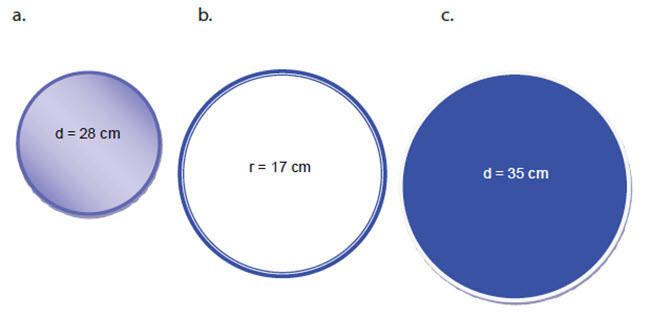
1. Hitunglah keliling bulat berikut !
| a. K = | 22 | x 28 = 88 cm |
| 7 |
b. K = 2πr = 2 x 3,14 x 17 = 106,76
| c. K = | 22 | x 35 = 110 cm |
| 7 |
2. Hitunglah jari-jari pada bulat berikut!
| a. r = | K | = | 628 | = 100 cm |
| 2 x 3,14 | 6,28 |
| b. r = | K | = | 50 | = 7,96 cm |
| 2 x 3,14 | 6,28 |
| c. r = | K | = | 132 | = 21 cm |
| 2 x 3,14 | 6,28 |
3. Tentukan keliling pada gambar berikut!
a. Sebuah pelangi diketahui jari-jarinya 26 cm.
Diketahui:
jari-jari pelangi = 26 cm
Ditanya:
Keliling pelangi = … ?
Jawab:
| K = | 1 | x 2πr |
| 2 |
| K = | 1 | x 2 x 3,14 x 26 |
| 2 |
| K = | 1 | x 163,28 = 81,64 |
| 2 |
b. Sebuah mainan diketahui diameternya 14 cm.
| K = | 22 | x 14 = 44 cm |
| 7 |
4. Sebuah taman berbentuk lingkaran. Lingkaran tersebut memiliki diameter 98 m. Setiap jarak 11 m pada pinggir taman ditanami pohon palm. Tentukan banyaknya pohon palm yang diperlukan
Diketahui:
Taman berbentuk bundar
Diameter taman = 98 m
Sekelilingnya ditanami pohon palm dengan jarak 11 m
Ditanya:
Banyak pohon palm yang diharapkan = … ?
Jawab:
Banyak pohon palm yang diperlukan
= keliling taman : jarak antar pohon
= π x d : 11
= 22/7 x 98 : 11
= 22 x 14 : 11
= 308 : 11
= 28 pohon palm
Makara banyak pohon palm yang dibutuhkan adalah 28 batang.
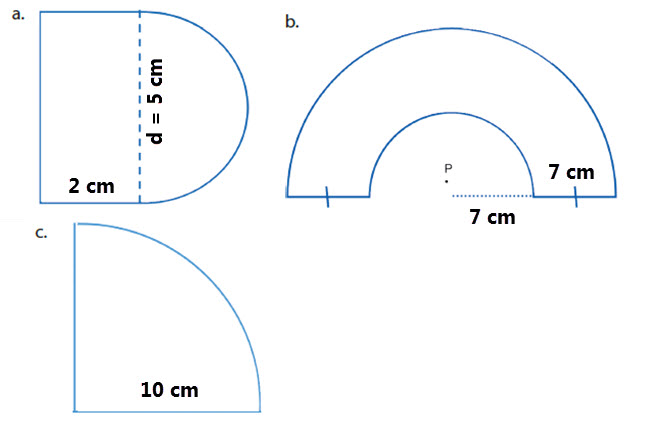
5. Hitunglah keliling bangkit berikut!
a. Keliling berdiri mampu dicari dengan cara sebagai berikut
Keliling 1/2 lingkaran
Diketahui :
Diameter = 5 cm
| K = | 1 | πd |
| 2 |
| K = | 1 | x 3,14 x 5 |
| 2 |
| K = | 1 | x 15,7 = 7,85 |
| 2 |
Keliling berdiri = 2 + 5 + 2 + 7,85 = 16,85 cm
b. Keliling bangun dapat dicari dengan cara sebagai berikut.
Keliling 1/2 bulat besar
Diketahui :
r = 14 cm
π = 22/7
| K = | 1 | x 2πr |
| 2 |
| K = | 1 | x 2 x | 22 | x 14 |
| 2 | 7 |
| K = | 1 | x 88 = 44 |
| 2 |
Keliling 1/2 lingkaran kecil
Diketahui :
r = 7 cm
π = 22/7
| K = | 1 | x 2πr |
| 2 |
| K = | 1 | x 2 x | 22 | x 7 |
| 2 | 7 |
| K = | 1 | x 44 = 22 |
| 2 |
Keliling Bangun = 44 + 22 + 7 + 7 = 80 cm
c. Keliling bangkit mampu dicari dengan cara sebagai berikut.
Diketahui :
r = 10 cm
π = 3,14
K = 2πr
K = 2 x 3,14 x 10
K = 62,8
Kelililing bangkit = 10 + 10 + 62,8 = 82,8.
Terima kasih telah membaca artikel di website kabarpandeglang.com, semoga bisa memberikan informasi yang bermanfaat bagi kamu dan bisa dijadikan referensi. Artikel ini telah dimuat pada kategori pendididkan https://kabarpandeglang.com/topik/pendidikan/, Jangan lupa share ya jika artikelnya bermanfaat. Salam admin ganteng..!!