KABARPANDEGLANG.COM – Lingkaran yaitu kumpulan titik-titik pada bidang datar. Titik-titik tersebut mempunyai jarak sama terhadap suatu titik tertentu.Luas lingkaran yaitu tempat yang dilingkupi oleh bulat. Untuk menghitung luas bulat dibutuhkan panjang jari-jari lingkaran. Selain itu dipakai juga pi yang mempunyai nilai 22/7 atau 3.14.
A. Luas Lingkaran dengan Pendekatan Persegi Panjang.
Salah satu cara menemukan luas lingkaran ialah dengan memakai pendekatan persegi panjang. Semakin banyak juring maka akan semakin membentuk persegi panjang yang lebih mendekati dengan syarat jumlahnya genap dan jangan lupa salah satu juring dibagi dua sama berdasarkan jari-jari. Langkah mencari luas bulat dengan pendekatan persegi panjang adalah sebagai berikut.
- Gambarlah lingkaran pada kertas karton. Gunakan jangka. Warnailah daerah dalam bulat tersebut.
- Potonglah lingkaran mirip pada gambar. Kemudian, lipat lingkaran sehingga menghasilkan setengah lingkaran. Lipat kembali setengah lingkaran tersebut menjadi seperempat lingkaran. Untuk ketiga kalinya, lipat seperempat bulat menjadi seperdelapan bundar. Terakhir, lipat seperdelapan bulat menjadi seperenam belas bundar.
- Kemudian, potong bulat berdasarkan lipatan yang telah dihasilkan. Potongan-serpihan tersebut merupakan juring lingkaran.
- Susunlah juring-juring yang dihasilkan. Kemudian, potonglah salah satu juring menjadi dua bab. Dengan demikian, akan membentuk bangun menyerupai persegi panjang.
- Bangun yang dihasilkan ibarat persegi panjang. Jadi, luas lingkaran yang dimaksud sama dengan luas persegi panjang. Dimana panjangnya mendekati πr (keliling setengah bundar) dan lebarnya r. Dengan demikian, diperoleh Luas bulat sebagai berikut.
L Lingkaran = Luas persegipanjang
L Lingkaran = p x l
L Lingkaran = πr x r
L bundar = πr²
Luas lingkaran dirumuskan dengan L = π r²
Keterangan
L ialah tempat luas bundar
r adalah panjang jarijari bundar
π ialah 3,14 atau 22/7
Berikut ini video perihal mencari luas bulat dengan pendekatan persegipanjang, segitiga dan belah ketupat.
B. Luas Lingkaran dengan Pendekatan Segitiga
Pembuktian Rumus Luas Daerah Lingkaran Juga dapat memakai Luas Daerah Segitiga Lingkaran dipotong-potong 16 juring. Kemudian juring-juring tersebut disusun menjadi bentuk segitiga samakaki.
Sehingga terbentuk segitga sama kaki dengan panjang alas = ¼ keliling lingkaran dan tinggi = 4r.
Luas Segitiga = 1/2 x ganjal x tinggi
| = | 1 | ( | 1 | keliling laingkaran x 4r) |
| 2 | 4 |
| = | 1 | (2πr) x 4r |
| 8 |
| = | 1 | πr x 4r |
| 4 |
= π r²
C. Menentukan Jari-jari Jika Diketahui Luas
Rumus dari luas bundar yakni = π x r² maka bila akan mencari jari-jarinya rumusnya yakni
| r =√ | L |
| π |
L merupakan luas
r merupakan jari-jari
π = 22/7 atau 3.14
Perhatikan contoh berikut ini. Sebuah bundar mempunyai luas 314 cm². Berapakah jari-jari lingkaran tersebut?
L = πr²
314 = 3,14 r²
r² = 314/3,14
r² = 100
r x r = 10 x 10
r = 10
Makara, panjang jari-jari lingkaran yaitu 10 cm
D. Menentukan Luas Lingkaran Jika Diketahui Keliling
Jika ingin mencari luas, maka harus diketahui jari-jarinya dahulu. Jari jari dapat dicari dari rumus keliling yaitu 2πr atau πd. Perhatikan teladan berikut ini. Sebuah bundar memiliki keliling 44 cm. Hitunglah luas lingkaran tersebut!
Diketahui :
Keliling = 44 cm
π = 22/7
Ditanya : Luas…??
Jawab :
| K = 2πr sehinga r = | K |
| 2π |
| r = | K |
| 2π |
| r = | 44 |
| 2 x 22/7 |
| r = | 44 |
| 44/7 |
| r = 44 : | 44 |
| 7 |
r = 7 cm
Jika jari-jari bulat 7 cm, maka luas bundar yakni
L = π r²
| L = | 22 | x 7 x 7 |
| 7 |
L = 22 x 7
L = 154
Kaprikornus, luas bulat tersebut yakni 154 cm².
Ayo Mencoba
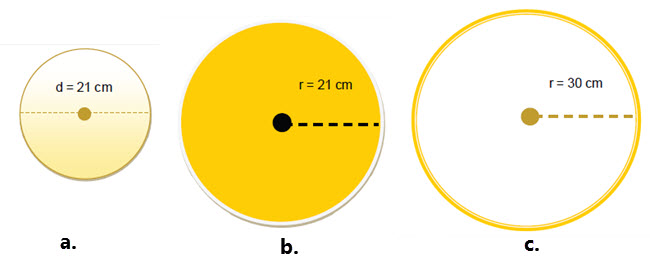
1. Hitunglah luas lingkaran berikut
a. Diketahui :
Diameter = 21 cm maka r = 10,5
π = 22/7
Ditanya : Luas ?
L = π r²
| L = | 22 | x 10,5 x 10,5 |
| 7 |
L = 346,5 cm²
b. Diketahui :
r = 21 cm
π = 22/7
Ditanya : Luas = ?
L = πr²
| L = | 22 | x 21 x 21 |
| 7 |
L = 1.386 cm²
c. Diketahui :
r = 30 cm
π = 3,14
Ditanya : Luas = ?
L = πr²
L = 3,14 x 30 x 30
L = 2.826 cm²
2. Diketahui luas bundar 1.386 cm². Berapakah jari-jari bundar tersebut?
Diketahui :
L = 1.386 cm
ditanya jari2 .
maka :
L = π r²
1386 = 22/7 x r²
r² = 441
r = 21 cm
3. Sebuah bundar mempunyai keliling 94,2 cm. Hitunglah
a. diameter bundar,
Diketahui:
Keliling bulat = 94,2 cm
Ditanya: Diameter bulat
Jawab:
Keliling bulat = π x d
94,2 = 3,14 x d
d = 94,2 : 3,14
d = 30 cm
b. jari-jari bulat,
Diketahui:
Keliling bulat = 94,2 cm
Ditanya: jari-jari bundar
Jawab:
Keliling bundar = 2 x π x r
94,2 = 2 x 3,14 x r
94,2 = 6,28 x r
r = 94,2 : 6,28
r = 15 cm
c. luas lingkaran.
Diketahui:
Keliling lingkaran = 94,2 cm
Ditanya: Luas lingkaran
Jawab:
Luas = π x r²
= 3,14 x 15 x 15
= 706,5 cm²
4. Diketahui jari-jari dua bundar r1 dan r2 yang selisih luasnya tidak lebih dari 50 cm². Hitunglah jari-jari dua bulat r1 dan r2 Tersebut.
Diketahui
Jika r1 = 7 cm
Dan r2 = 8 cm
Maka
r1 = 22/7 × 7 × 7 = 154cm²
r2= 3,14 × 8 × 8 = 200,96
Kemudian Dikurangkan
200,96 – 154 = 46,96
Selisihnya yaitu 46,96 selisih tersebut tidah lebih dari 50 cm²
Terima kasih telah membaca artikel di website kabarpandeglang.com, semoga bisa memberikan informasi yang bermanfaat bagi kamu dan bisa dijadikan referensi. Artikel ini telah dimuat pada kategori pendididkan https://kabarpandeglang.com/topik/pendidikan/, Jangan lupa share ya jika artikelnya bermanfaat. Salam admin ganteng..!!