KABARPANDEGLANG.COM – Lingkaran yakni himpunan semua titik di sebuah bidang datar mempunyai jarak yang sama dari suatu titik tetap pada bidang tersebut. Titik tetap pada bidang itu disebut dengan titik sentra bundar. Adapun jarak yang sama dari satu titik ke titik yang lain disebut dengan jari-jari (radius) lingkaran.
Bidang bundar yakni daerah yang dibatasi dengan bundar. Tentu saja berbeda antara bundar dan bidang bundar. Dengan benang kita mampu mengkontekstualkan lingkaran sedangkan dengan tripleks atau karton dapat mengkontekstualkan bidang bundar.
Menggambar Lingkaran
Untuk membuat sebuah bundar, diperlukan sebuah jangka dan penggaris. Mula-mula ukurlah panjang radius (jari-jari) yang diinginkan pada sebuah penggaris dengan memakai jangka. Lalu pindahkan jangka tersebut dari penggaris, dan mulailah membuat sebuah lingkaran pada kertas yang lain.
Pastikanlah, bagian lancip pada jangka menancap cukup kuat pada kertas sehingga tidak bergeser. Putarlah pangkal kepala jangka dengan hati-hati, putaran dari titik awal sampai kembali ke titik awal.
1. Bagian-bab Lingkaran
Lingkaran memiliki bab-bab yang membentuk sebuah bulat. Bagian-bagian lingkaran antara lain sebagai berikut.
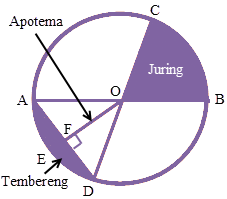
- Titik Pusat bundar yaitu titik yang terletak di tengah-tengah bulat. Pada gambar di samping titik O merupakan titik sentra lingkaran.
- Jari-jari bulat (r) adalah garis dari titik sentra bundar ke lengkungan bulat. Pada gambar disampingd jari-jari bulat ditunjukkan oleh garis OA, OB, OC, dan OD.
- Diameter (d) yaitu garis lurus yang menghubungkan dua titik pada lengkungan bundar dan melalui titik sentra. Pada gambar disamping AB dan CD merupakan diameter bulat. Panjang diameter lingkaran ialah 2 kali panjang jari-jari bulat atau bisa ditulis d = 2r.
- Busur lingkaran yaitu garis lengkung yang terletak pada lengkungan lingkaran dan menghubungkan dua titik sebarang di lengkungan tersebut. Pada gambar di atas, garis lengkung AC (ditulis) merupakan busur bulat. Busur bulat dibagi menjadi 2, adalah busur kecil dan busur besar. Pada umumnya, istilah dalam buku hanya busur bundar. Ini berarti yang dimaksud yakni busur kecil.
- Tali busur bundar yaitu garis lurus dalam bulat yang menghubungkan dua titik pada lengkungan lingkaran dan tidak melalui pusat bulat. Tali busur yang melalui sentra bundar dinamakan dengan diameter bundar. Tali busur bulat tersebut ditunjukkan oleh garis lurus AD yang tidak melalui titik sentra seperti pada gambar di atas.
- Tembereng yakni luas kawasan dalam lingkaran yang dibatasi oleh busur dan tali busur. Pada Gambar di atas, tembereng ditunjukkan oleh kawasan yang diarsir dan dibatasi oleh busur AD dan tali busur AD. Kaprikornus tembereng terbentuk dari campuran antara busur bundar dengan tali busur bulat.
- Juring bundar yaitu luas daerah dalam bundar yang dibatasi oleh dua buah jari-jari bulat dan sebuah busur yang diapit oleh kedua jari-jari bulat tersebut. Pada Gambar di atas, juring bundar ditunjukkan oleh kawasan yang diarsir yang dibatasi oleh jari-jari OC dan OB serta busur BC, dinamakan juring BOC.
- Apotema bundar merupakan garis yang menghubungkan titik pusat bundar dengan tali busur bundar tersebut. Garis yang dibuat bersifat tegak lurus dengan tali busur. Coba perhatikan Gambar di atas secara seksama. Garis OF merupakan garis apotema pada lingkaran O.
2. Diameter

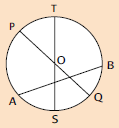
Diameter bundar (d) yaitu ruas garis yang menghubungkan dua titik pada busur bulat melalui titik pusat lingkaran. Diameter disebut juga dengan garis tengah. Perhatikan gambar di samping.
PQ dan ST melewati sentra lingkaran O. Maka POQ disebut sebagai diameter bundar tersebut. POQ dan SOT memiliki panjang yang sama, maka SOT juga disebut dengan diameter. Tetapi perhatikan garis AB ! AB bukan diameter karena tidak melalui sentra bundar. OP dan OQ adalah jari-jari lingkaran. OP = OQ PQ = 2 x OP atau PQ = 2 x OQ.
Diameter = 2 x jari-jari lingkaran
Jari-jari lingkaran = diameter : 2
3. Phi (π)
Pi ialah suatu tetapan yang dipakai untuk mencari luas lingkaran. Nilai Pi yaitu suatu besaran yang merupakan sifat khusus dari bulat, yaitu perbandingan dari keliling (K) dengan diameternya (d). Nilai perbandingan antara keliling dan diameter bundar ini selalu konstan untuk setiap bulat adalah 3,14159265358 atau 22/7. Pi ialah panjang keliling bundar yang berdiameter 1 satuan. Perhatikan acuan berikut.
| No. | Diameter | Keliling Lingkaran | Keliling : Diameter | ||||
|---|---|---|---|---|---|---|---|
| 1. | 7 cm |
|
22 : 7 = 3.142857142857143 | ||||
| 2. | 14 cm |
|
44 : 14 = 3.142857142857143 | ||||
| 3. | 21 cm |
|
66 : 21 = 3.142857142857143 | ||||
| 4. | 28 cm |
|
88 : 28 = 3.142857142857143 |
3. Keliling Lingkaran
Apabila keliling lingkaran dibagi dengan panjang diameternya, akan menghasilkan nilai yang sama. Angka tersebut dinamakan pi (π). Nilai pi adalah 3,14159265358 atau 22/7
Keliling bundar : diameter = π.
Maka: Keliling bundar = π x diameter atau πd
Soal Latihan :
1. Dengan menggunakan π = 22/7 tentukan keliling bundar yang memiliki:
a. Diameter 14 cm
| K = πd = | 22 | x 14 = 44 cm |
| 7 |
b. radius 21 cm, d = 2 x 21 = 42
| K = πd = | 22 | x 42 = 132 cm |
| 7 |
d. Diameter 63 cm
| K = πd = | 22 | x 63 = 198 cm |
| 7 |
e. radius 28 cm, d = 2 x 28 = 56 cm
| K = πd = | 22 | x 56 = 176 cm |
| 7 |
f. radius 12 cm
| K = πd = | 22 | x 12 = 37,71 cm |
| 7 |
2. Dengan memakai π = 3,14, tentukan keliling bulat yang memiliki:
a. Diameter 20 cm
K = πd = 3,14 x 20 = 62,8 cm
b. radius 20 cm, d = 2 x 20 = 40
K = πd = 3,14 x 40 = 125,6 cm
c. Diameter = 12 cm
K = πd = 3,14 x 12 = 37,68 cm
d. Diameter = 16 cm
K = πd = 3,14 x 16 = 50,24 cm
d. Jari-jari = 7 cm, d = 2 x 7 = 14 cm
K = πd = 3,14 x 14 = 43,96 cm
4. Mencari Luas Lingkaran
Luas bulat yakni bidang yang dibatasi oleh garis yang berjarak sama ke titik pusat bundar. Untuk menemukan luas bulat dapat menggunakan langkah-langkah mirip di bawah ini :
- Buatlah sebuah bulat dengan diameter tertentu.
- Lalu lipatlah sedemikian rupa sampai menjadi 8 bab.
- Bukalah lipatan lingkaranmu dan kamu akan mendapatkan bab bundar yang sama.
- Buatlah garis mengikuti garis lipatan pada kertas.
- Potonglah setiap bagian bundar dengan memakai gunting secara hatihati.
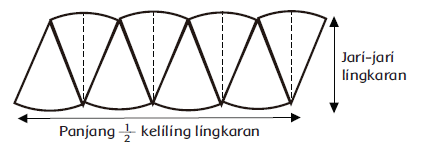
- Letakkan kepingan bab lingkaran mengikuti gambar di bawah ini.
- Lalu ambillah satu bab yang berada di paling pinggir.
- Lipatlah bab itu sehingga menjadi dua bagian yang sama.
- Potonglah kedua bab tersebut dengan memakai gunting.
- Lalu ambillah satu bab dan letakkanlah di samping kiri jajaran belahan lingkaranmu sebelumnya.
- Letakkan bab yang lain di sisi kanan.
- Maka kau akan melihat jajaran bagian lingkaran itu membentuk sebuah persegi panjang.
Luas bulat = luas persegi panjang
= panjang x lebar
= π x jari-jari x jari-jari (jari-jari = radius)
= π x r²
Dengan demikian, maka: Luas Lingkaran = π x r²
Contoh :
a. Hitunglah luas lingkaran berikut yang mempunyai radius 12 cm (π = 3,14)
Luas bundar = π x radius x radius
= 3,14 X 12 X 12
= 452,16 cm²
b. Diameter sebuah cakram berbentuk lingkaran ialah 18 cm. Berapakah luas cakram tersebut?
Radius bundar cakram = 18 : 2 = 9 cm
Luas bundar cakram = π x radius x radius
= π x 9 x 9
= 3,14 x 81
= 254,34 cm²
c. Diameter sebuah lingkaran ialah 14 meter. Berapakah luas lingkaran tersebut? (π = 22/7)
Radius bundar = 14 : 2 = 7 m
Luas lingkaran = π x radius x radius
| Luas = | 22 | x 7 x 7 = 154 m² |
| 7 |
Perhatikan contoh berikut :
| No. | d | π = 22/7 | π = 3,14 | ||||
|---|---|---|---|---|---|---|---|
| 1. | 14 cm |
|
L=πxrxr = 3,14 x 14×14 =615,44 cm² | ||||
| 2. | 21 cm |
|
L=πxrxr = 3,14 x 21×21 =1.384, 74 cm² | ||||
| 3. | 28 cm |
|
L=πxrxr = 3,14 x 28×28 =2.461, 76 cm² | ||||
| 4. | 35 cm |
|
L=πxrxr = 3,14 x 35×35 =3.846, 5 cm² |
Dengan memperhatikan contoh di atas apabila jari-jari atau diameter adalah bilangan kelipatan 7 sebaiknya menggunakan π = 22/7 dan apabila diameter atau jari-jari bukan kelipatan 7 sebaiknya menggunakan π = 3,14.
Terima kasih telah membaca artikel di website kabarpandeglang.com, semoga bisa memberikan informasi yang bermanfaat bagi kamu dan bisa dijadikan referensi. Artikel ini telah dimuat pada kategori pendididkan https://kabarpandeglang.com/topik/pendidikan/, Jangan lupa share ya jika artikelnya bermanfaat. Salam admin ganteng..!!