Sifat-Sifat Bangkit Ruang

KABARPANDEGLANG.COM – Euclid adalah seorang matematikawan kuno. Dia berasal dari Alexandria, Mesir (325 – 265 SM). Euclid menghasilkan sebuah karya monumental dalam bidang geometri, adalah buku yang berjudul The Elements. Buku tersebut memuat konsep geometri dan teori bilangan. Buku The Elements menjadi buku teks di sekolah pada waktu itu.

Hampir dua ribu tahun unsur-unsur karya Euclid dipandang sebagai suatu model akal sehat matematika. Sejak dikala itu pelajaran perihal unsur-unsur dari buku The elements menjadi bab yang penting dalam pendidikan. Unsur-unsur tersebut diajarkan dari generasi ke generasi dengan menggunakan pedoman deduktif. Makara, materi geometri yang akan kita pelajari berikut ini sebagian besar merupakan hasil karya Euclid.

Bangun ruang yaitu bangkit geometri dimensi tiga yang mempunyai sifat-sifat tertentu, ialah mempunyai sisi, rusuk, dan titik sudut. Materi berdiri ruang yang akan dipelajari pertama yaitu prisma.

A. Prisma

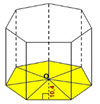
Prisma adalah bangun ruang yang dibatasi oleh dua buah sisi (bidang) sejajar serta beberapa sisi (bidang)yang saling berpotongan menurut garisgaris yang sejajar. Dua sisi (bidang) yang sejajar tersebut dinamakan sisi (bidang) ganjal dan sisi (bidang) atas. Sisi-sisi lainnya disebut dengan sisi (bidang) tegak, sedangkan jarak antara kedua sisi (bidang) disebut tinggi prisma.

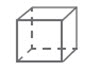
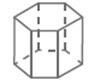
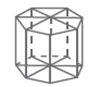
Prisma yang rusuk tegaknya tegak lurus pada sisi (bidang) alasnya disebut prisma tegak. Sisi (bidang) alasnya berbentuk segi banyak (segitiga, segi empat, segi lima, segi enam, ….) dan bentuknya bebas, artinya sisi (bidang) alasnya tidak harus berbentuk persegi panjang, persegi atau bentuk yang istimewa lainnya. Dengan memperhatikan pengertian prisma tegak seperti di atas, sebenarnya kubus dan balok termasuk prisma tegak.

Dalam prisma tegak, bidang sisi tegaknya berbentuk persegi panjang atau persegi. Prisma dengan bantalan dan tutup berbentuk persegi disebut balok sedangkan prisma dengan alas dan tutup berbentuk bundar disebut tabung. Sifat-sifat prisma sebagai berikut.

1. Prisma terdiri atas sisi bantalan dan sisi atas yang bentuk dan ukurannya sama.
2. Mempunyai sisi bantalan dan sisi atas yang sejajar.
3. Mempunyai sisi-sisi tegak yang berbentuk persegi panjang.
4. Jarak antara sisi alas dan sisi atas disebut tinggi prisma.

No.	Gambar	Jenis Prisma	Banyak Sisi Tegak	Jumlah Sisi	Jumlah Rusuk
1		Prisma segitiga	3	5	9
2		Prisma segi empat	4	6	12
3		Prisma segi lima	5	7	15
4		Prisma segi enam	6	8	18
5		Prisma segi-n	n	n + 2	3n
6		Prisma segi tujuh	7	7 + 2 = 9	3 x 7 = 21

Kesimpulan :

Jenis-jenis prisma didasarkan pada bentuk sisi (bidang) bantalan atau jumlah sisi (bidang) tegak. Jika sisi alas berbentuk segitiga maka prismanya disebut prisma segitiga atau jikalau jumlah sisi (bidang) tegak ada tiga maka disebut prisma segitiga. Jika bidang alas berbentuk segi empat maka prismanya disebut prisma segi empat. Jika bidang bantalan berbentuk segi-n maka prismanya disebut prisma segi-n.

No.	Jenis Prisma	Sifat-Sifat
1	Prisma segitiga	Memiliki sisi alas dan sisi atas berupa segitiga yang kongruen (2 sisi tersebut juga merupakan sisi prisma segitiga). Memilki 3 sisi tegak yang semuanya berbentuk segi empat. Memiliki 9 rusuk. Memiliki 6 titik sudut.
2	Prisma segi empat	Memiliki sisi (bidang) ganjal dan sisi (bidang) atas berupa segi empat yang kongruen (2 bantalan tersebut juga merupakan sisi prisma segi empat) Memilki 6 sisi (2 sisi berupa sisi atas dan sisi alas, 4 sisi lainnya merupakan sisi tegak yang semuanya berbentuk segi empat) Memiliki 12 rusuk Memiliki 8 titik sudut
3	Prisma segi lima	Memiliki sisi (bidang) bantalan dan sisi (bidang) atas berupa segi lima yang kongruen (2 alas tersebut juga merupakan sisi prisma segi lima) Memilki 7 sisi (2 sisi berupa sisi atas dan sisi bantalan, 5 sisi lainnya merupakan sisi tegak yang semuanya berbentuk segi empat) Memiliki 15 rusuk Memiliki 10 titik sudut
4	Prisma segi enam	Memiliki sisi (bidang) bantalan dan sisi (bidang) atas berupa segi enam yang kongruen (2 ganjal tersebut juga merupakan sisi prisma segi lima) Memilki 8 sisi (2 sisi berupa sisi atas dan sisi ganjal, 6 sisi lainnya merupakan sisi tegak yang semuanya berbentuk segi empat) Memiliki 18 rusuk Memiliki 12 titik sudut
5	Prisma segi tujuh	Memiliki sisi (bidang) ganjal dan sisi (bidang) atas berupa segi enam yang kongruen (2 ganjal tersebut juga merupakan sisi prisma segi tujuh) Memilki 9 sisi (2 sisi berupa sisi atas dan sisi alas, 7 sisi lainnya merupakan sisi tegak yang semuanya berbentuk segi empat) Memiliki 21 rusuk Memiliki 14 titik sudut
6	Prisma segi delapan	Memiliki sisi (bidang) ganjal dan sisi (bidang) atas berupa segi enam yang kongruen (2 ganjal tersebut juga merupakan sisi prisma segi delapan) Memilki 10 sisi (2 sisi berupa sisi atas dan sisi bantalan, 8 sisi lainnya merupakan sisi tegak yang semuanya berbentuk segi empat) Memiliki 24 rusuk Memiliki 16 titik sudut
7	Prisma segi sembilan	Memiliki sisi (bidang) alas dan sisi (bidang) atas berupa segi enam yang kongruen (2 bantalan tersebut juga merupakan sisi prisma segi sembilan) Memilki 11 sisi (2 sisi berupa sisi atas dan sisi ganjal, 9 sisi lainnya merupakan sisi tegak yang semuanya berbentuk segi empat) Memiliki 27  rusuk Memiliki 18 titik sudut
8	Prisma segi sepuluh	Memiliki sisi (bidang) ganjal dan sisi (bidang) atas berupa segi enam yang kongruen (2 bantalan tersebut juga merupakan sisi prisma segi sepuluh) Memilki 12 sisi (2 sisi berupa sisi atas dan sisi ganjal, 10 sisi lainnya merupakan sisi tegak yang semuanya berbentuk segi empat) Memiliki 30 rusuk Memiliki 20 titik sudut
9	Prisma segi-n	Memiliki sisi (bidang) alas dan sisi (bidang) atas berupa segi enam yang kongruen (2 bantalan tersebut juga merupakan sisi prisma segi-n) Memilki n sisi (2 sisi berupa sisi atas dan sisi bantalan, n sisi lainnya merupakan sisi tegak yang semuanya berbentuk segi empat) Memiliki 3n rusuk Memiliki 2n titik sudut

B. Tabung

Tabung ialah suatu bangkit ruang yang dibatasi oleh dua lingkaran yang sejajar dan kongruen dan dibatasi juga oleh himpunan (atau kawasan kedudukan) garis-garis sejajar yang tegak lurus dan memotong dua bulat tersebut.

Tabung ialah permukaan tertutup sederhana yang batasnya berupa bagian dari pada tabung dan alasnya berupa lingkaran. Suatu tabung bulat mampu dipandang sebagai suatu prisma khusus alasnya berupa daerah lingkaran. Kaprikornus tabung merupakan prisma yang ganjal dan tutupnya berbentuk bundar. Sifat-sifat tabung sebagai berikut.

1. Tabung mempunyai sisi sebanyak 3 buah, yaitu sisi atas, sisi bantalan, dan selimut tabung.
2. Tidak mempunyai titik sudut.
3. Sisi (bidang) atas dan sisi (bidang) bantalan berbentuk bulat dengan ukuran sama.
4. Memiliki sisi lengkung yang disebut selimut tabung.
5. Jarak bidang atas dan bidang alas disebut tinggi tabung.
6. Memiliki 2 rusuk lengkung.

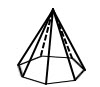
C. Limas

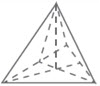
Limas ialah suatu bangun ruang yang dibatasi oleh sebuah segi-n (yang disebut dengan bidang bantalan) dan beberapa segitiga (yang disebut dengan sisi tegak) yang mempunyai satu titik sudut komplotan (yang disebut dengan puncak).

Rusuk-rusuk yang melalui puncak disebut dengan rusuk tegak. Penamaan limas bergantung dari bentuk alasnya. Karena sisi tegaknya berbentuk segitiga, maka limas tidak mempunyai sisi atas, tapi mempunyai klimaks. Sifat-sifat limas sebagai berikut.

1. Mempunyai sisi tegak berbentuk segitiga
2. Sisi alasnya berbentuk segi banyak.
3. Mempunyai satu klimaks.
4. Penamaan limas tergantung bentuk alasnya.

No.	Gambar	Jenis Limas	Banyak Sisi Tegak	Jumlah Sisi	Jumlah Rusuk
1		Limas segitiga	3	4	6
2		Limas segi empat	4	5	8
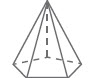
3		Limas segi lima	5	6	10
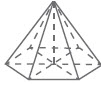
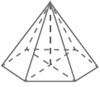
4		Limas segi enam	6	7	12
5		Limas segi-n	n	n + 1	2n
6		Limas segi tujuh	7	7 + 1 = 8	2 x 7 = 14

Kesimpulan

Jenis limas ditentukan dari bentuk bidang alasnya atau banyaknya sisi tegak. Jika bidang alasnya berbentuk segitiga maka limasnya disebut limas segitiga atau jikalau banyaknya sisi tegak ada tiga maka disebut limas segitiga. Jika bidang alasnya berbentuk segi empat maka limasnya disebut limas segi empat. Jika bidang alasnya berbentuk segi-n maka limasnya disebut limas segi-n.

No.	Jenis Prisma	Sifat-Sifat
1	Limas segitiga	Memiliki 4 sisi yang berbentuk segitiga (1 merupakan ganjal yang berbentuk segitiga dan 3 sisi tegak) Memiliki 6 rusuk Memiliki 4 titik sudut ( 3 sudut berada di bab ganjal dan 1 sudut berada di bab atas yang merupakan titik puncak)
2	Limas segi empat	Memiliki 5 sisi  (1 sisi merupakan bantalan yang berbentuk segiempat dan 3 berupa segitiga yang merupakan sisi tegak) Memiliki 8 rusuk Memiliki 5 titik sudut ( 4 sudut berada di bab alas dan 1 sudut berada di bagian atas yang merupakan klimaks)
3	Limas segi lima	Memiliki 6 sisi  (1 sisi merupakan bantalan yang berbentuk segilima dan 5 sisi berupa segitiga yang merupakan sisi tegak) Memiliki 10 rusuk Memiliki 6 titik sudut ( 5 sudut berada di bab bantalan dan 1 sudut berada di bab atas yang merupakan klimaks)
4	Limas segi enam	Memiliki 7 sisi  (1 sisi merupakan alas yang berbentuk segienam dan 6 sisi berupa segitiga yang merupakan sisi tegak) Memiliki 12 rusuk Memiliki 7 titik sudut (6 sudut berada di bagian bantalan dan 1 sudut berada di bab atas yang merupakan titik puncak)
5	Limas segi tujuh	Memiliki 8 sisi  (1 sisi merupakan alas yang berbentuk segitujuh dan 7 sisi berupa segitiga yang merupakan sisi tegak) Memiliki 14 rusuk Memiliki 8 titik sudut (7 sudut berada di bagian ganjal dan 1 sudut berada di bagian atas yang merupakan titik puncak)
6	Limas segi delapan	Memiliki 9 sisi  (1 sisi merupakan bantalan yang berbentuk segidelapan dan 8 sisi berupa segitiga yang merupakan sisi tegak) Memiliki 16 rusuk Memiliki 9 titik sudut (8 sudut berada di bagian ganjal dan 1 sudut berada di bab atas yang merupakan klimaks)
7	Limas segi sembilan	Memiliki 10 sisi  (1 sisi merupakan bantalan yang berbentuk segisembilan dan 9 sisi berupa segitiga yang merupakan sisi tegak) Memiliki 18 rusuk Memiliki 10 titik sudut (9 sudut berada di bab alas dan 1 sudut berada di bab atas yang merupakan titik puncak)
8	Limas segi sepuluh	Memiliki 11 sisi  (1 sisi merupakan bantalan yang berbentuk segisepuluh dan 9 sisi berupa segitiga yang merupakan sisi tegak) Memiliki 20 rusuk Memiliki 11 titik sudut (10 sudut berada di bagian ganjal dan 1 sudut berada di bab atas yang merupakan titik puncak)
9	Limas segi-n	Memiliki n+1 sisi  (1 sisi merupakan ganjal yang berbentuk segi-n dan n-1 sisi berupa segitiga yang merupakan sisi tegak) Memiliki 2n rusuk Memiliki n+1 titik sudut (n sudut berada di bab alas dan 1 sudut berada di bab atas yang merupakan titik puncak)

D. Kerucut

Kerucut ialah suatu bangun ruang yang dibatasi oleh sebuah bundar (yang disebut bidang ganjal) dan dibatasi juga oleh himpunan (atau tempat kedudukan) garis-garis yang melalui suatu titik (yang disebut puncak) dan juga melalui bundar tadi.

Kerucut ada juga yang mengartikan yaitu berdiri ruang yang dibatasi oleh sebuah sisi ganjal yang berbentuk lingkaran dan sebuah sisi lengkung (selimut yang mengerucut ke atas, semakin ke atas semakin kecil atau lancip). Sifat-sifat kerucut sebagai berikut.

1. Alasnya berbentuk bundar.
2. Memiliki sisi lengkung yang disebut selimut kerucut.
3. Sisi kerucut ada 2, ialah bundar (bawah), dan bidang melengkung yang disebut selimut kerucut.
4. Memiliki 1 rusuk lengkung.
5. Memiliki sebuah titik puncak.
6. Jarak klimaks ke bantalan disebut tinggi kerucut.

E. Bola

Bola yaitu bangun ruang tiga dimensi yang dibuat oleh tak sampai lingkaran berjari-jari sama panjang dan berpusat pada satu titik yang sama. Bola hanya mempunyai 1 sisi. bola merupakan berdiri ruang (permukaannya rapat dan bab dalamnya kosong). Semua titik pada sisinya (permukaan berdiri ruang itu) berjarak sama ke titik sentra.Bangun ruang bola memiliki sifat-sifat sebagai berikut.

1. Memiliki 1 sisi.
2. Memiliki 1 titik pusat.
3. Tidak mempunyai titik sudut.
4. Memiliki tak hingga jari-jari dan semuanya sama panjang.

Terima kasih telah membaca artikel di website kabarpandeglang.com, semoga bisa memberikan informasi yang bermanfaat bagi kamu dan bisa dijadikan referensi. Artikel ini telah dimuat pada kategori pendididkan https://kabarpandeglang.com/topik/pendidikan/, Jangan lupa share ya jika artikelnya bermanfaat. Salam admin ganteng..!!