KABARPANDEGLANG.COM – Materi pecahan di SD menitikberatkan pada pengerjaan (operasi) hitung dasar adalah penjumlahan, pengurangan, perkalian, dan pembagian, baik untuk kepingan biasa, adonan dan desimal. Untuk kelas V dan VI, bahan prasyarat yang seharusnya sudah dikuasai penerima bimbing yakni: konsep perkalian, operasi hitung penjumlahan kepingan, konsep pembagian, operasi hitung pengurangan kepingan, konsep pecahan gabungan, konsep kepingan desimal, konsep perkalian susun ke bawah, dan konsep pembagian susun ke bawah.
Sebelum melakukan operasi pengerjaan hitung pecahan sebaikya kita kenali terlebih dahulu banyak sekali bentuk kepingan yang akan dipelajari di SD. Ada beberapa macam bentuk cuilan yang digunakan di sekolah dasar. Selain mengenal berbagai bentuk belahan kita juga perlu mempelajari cara mengubah banyak sekali bentuk kepingan, menyederhanakan serpihan. Keterampilan mengubah berbagai bentuk bagian sangat berguna nantinya dalam pengerjaan hitung aneka macam bentuk potongan.
A. Memahami Berbagai Bentuk Pecahan
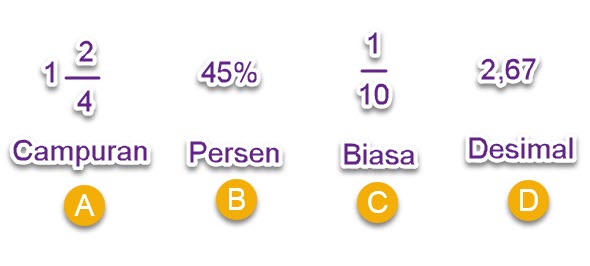
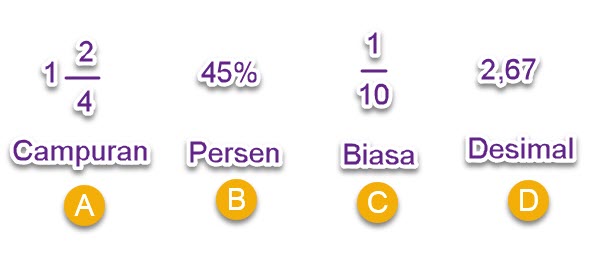
Pecahan ialah bilangan yang menggambarkan bagian dari suatu keseluruhan, bab dari suatu tempat, bab dari suatu benda atau bab suatu himpunan. Pecahan yang dipelajari di SD adalah pecahan biasa, serpihan campuran, belahan desimal, dan cuilan persen.
1. Pecahan biasa
Pecahan biasa yakni bilangan yang berbentuk a/b, dengan a, b bilangan bundar dan b ≠ 0. Dalam hal ini, a disebut pembilang dan b disebut penyebut
| Contoh : | 1 | , | 3 | (1 dan 3 disebut pembilang) | |
| 3 | 4 | (3 dan 4 disebut penyebut) |
2. Pecahan adonan
Pecahan adonan adalah campuran antara bilangan lingkaran dengan serpihan biasa. Suatu penggalan biasa yang pembilangnya lebih besar daripada penyebutnya mampu ditulis dalam bentuk cuilan adonan.
| Contoh potongan : | 6 | dapat ditulis dalam bentuk serpihan adonan |
| 4 |
| Penjelasan : | 6 | = 6 : 4 = 1 | 2 | atau 1 | 1 |
| 4 | 4 | 2 |
3. Pecahan desimal
Pecahan desimal merupakan bentuk lain dari penggalan. Pecahan desimal menyatakan nilai daerah per puluhan, per ratusan, per ribuan, dan seterusnya.
| Contoh : | 1 | bentuk belahan desimalnya adalah 0,1 |
| 10 |
4. Persen Persen
Pecahan persen yaitu bagian yang penyebutnya seratus dan dilambangkan dengan “%”. 15% dibaca lima belas persen, artinya 15/100. Setiap potongan biasa mampu diubah ke dalam bentuk persen dengan cara mengalikan pembilang kepingan tersebut dengan 100%.
| Contoh : | 1 | x 100 % = | 100 | % = 25% |
| 4 | 4 |
B. Mengubah Bentuk Pecahan
Sebelum mengubah banyak sekali bentuk belahan harus dikuasai terlebih dahulu cara menyederhanakan kepingan, karena biasanya penggalan yang diminta ialah penggalan dalam bentuk paling sederhana. Menyerhanakan serpihan biasa mampu dilakukan dengan cara membagi pembilang dan penyebut dengan bilangan yang sama.
| Contoh : | 20 | = | 20 : 2 | = | 10 |
| 6 | 6 : 2 | 3 |
1. Mengubah Pecahan biasa ke Pecahan Desimal atau Sebaliknya
Cara mengubah penggalan biasa ke kepingan desimal dapat dilakukan dengan cara mengubah penyebut menjadi 10, 100, atau 1000. Ingat, bahwa bilangan desimal merupakan bilangan per sepuluh, per seratus, atau per seribu.
| Contoh : | 1 | = | 1 x 25 | = | 25 | = 0,25 |
| 4 | 4 x 25 | 100 |
Untuk mengubah penggalan biasa juga mampu dilakukan dengan cara membagi langsung pembilang dengan penyebut.
Sebaliknya untuk mengubah serpihan desimal ke serpihan biasa mampu dilakukan dengan cara mengubah seperti di bawah ini.(ingat jumlah angka dibelakang koma memperlihatkan besarnya penyebut pecahan)
| Contoh 1: 0,75 = | 75 | = | 75 : 25 | = | 3 |
| 100 | 100 : 25 | 4 |
Contoh 2 : 2,58 = 2 satuan + 5 per sepuluhan + 8 per seratusan
| =2 + | 5 | + | 8 | = | 25 | = | 200 | + | 50 | + | 8 | = | 258 |
| 10 | 100 | 100 | 100 | 100 | 100 | 100 |
2. Mengubah Pecahan Biasa ke Pecahan Campuran atau Sebaliknya
Pecahan biasa yang dapat diubah ke serpihan adonan hanya cuilan biasa yang pembilangnya lebih besar daripada penyebutnya, Cara mengubahnya dengan cara membagi pembilang dengan penyebut (kesudahannya bilangan bulat), lalu sisa pembagian dijadikan pembilang bagian (penyebut tetap)
| Contoh : | 8 | = 8 : 3 (hasil 2 sisa 2) sehingga menjadi 2 | 2 |
| 3 | 3 |
Sebaliknya untuk mengubah penggalan gabungan ke bentuk cuilan biasa dapat dilakukan dengan cara mengalikan bilangan bundar dengan penyebut kemudian ditambah dengan pembilang, penyebut tetap.
| Contoh :2 | 2 | = (2 x 3) + 2 (pembilang) sehingga menjadi | 8 |
| 3 | 3 |
3. Mengubah Pecahan Biasa ke Persen atau Sebaliknya
Untuk mengubah potongan biasa ke bentuk persen mampu dilakukan dengan cara mengubah penyebut menjadi bilangan seratus, pembilang juga ikut dikalikan dengan bilangan yang dijadikan pengali penyebut.
| Contoh : | 2 | = (semoga menjadi 100 penyebut (5) dikalikan 20 | 2 x 20 | = | 40 | = 40% |
| 5 | 5 x 20 | 100 |
Sebaliknya untuk kmengubah serpihan persen ke belahan biasa mampu dilakukan dengan mengubah kepingan persen (perseratus) menjadi serpihan biasa kemudian apabila pecahan masih bisa disederhanakan, sederhanakanlah.
| Contoh 45% : | 45 | , sederhanakan membagi dengan bilangan yang sama | 45 : 5 | = | 9 |
| 100 | 100 : 5 | 20 |
C. Pengerjaan Hitung Bilangan Pecahan
Pengerjaan hitung serpihan mencakup penjumlahan, pengurangan, perkalian dan pembagian.
1. Penjumlahan dan Pengurangan Pecahan Pecahan Biasa
Penjumlahan potongan dapat dilakukan dengan cara menjumlahkan pembilang dengan pembilang, penyebut dengan penyebut. Jika penyebut belum sama, samakan terlebih dahulu dengan cara menggunakan KPK kedua penyebut.
| Contoh : | 2 | + | 1 | ,KPK 5 dan 3 ialah 15 (penyebut) = | (2 x 3)= 6 | + | (1 x 5) =5 | = | 11 |
| 5 | 3 | (5 x 3)=15 | (3 x 5)=15 | 15 |
Apabila penyebut dikalikan pada suatu bilangan, maka pembilang pun dikalikan pada bilangan yang sama. Untuk pecahan yang penyebutnya sama tinggal menjumlahkan pembilangnya saja, penyebutnya tetap (tidak usah dijumlahkan).
Untuk pengurangan caranya sama dengan penjumlahan hanya operasi hitungnya yang berbeda.
| Contoh : | 2 | – | 1 | ,KPK 5 dan 3 yaitu 15 (penyebut) = | (2 x 3)= 6 | – | (1 x 5) =5 | = | 1 |
| 5 | 3 | (5 x 3)=15 | (3 x 5)=15 | 15 |
2. Penjumlahan dan Pengurangan Pecahan Campuran
Penjumlahan serpihan campuran dapat dilakukan dengan dua cara adalah dengan mengubah serpihan gabungan menjadi potongan biasa terlebih dahulu atau dengan cara menjumlahkan bilangan bulat dengan bilangan lingkaran, belahan dengan potongan.
Cara 1 : (mengubah bagian campuran ke pecahan biasa)
| Contoh :2 | 2 | + 3 | 1 | = | 12 | + | 10 | = | 36 | + | 50 | = | 86 | = (86 : 15 = 5 sisa 11) = 5 | 11 |
| 5 | 3 | 5 | 3 | 15 | 15 | 15 | 15 |
Cara 2 : (bilangan bundar + bilangan bulat dan peahan + cuilan)
| Contoh :2 | 2 | + 3 | 1 | = 2 + 3 +( | 2 | + | 1 | ) = 5 +( | 6 | + | 5 | ) = 5 | 11 |
| 5 | 3 | 5 | 3 | 15 | 15 | 15 |
Untuk pengurangan caranya sama dengan penjumlahan hanya operasi hitungnya yang berbeda.
Cara 1 : (mengubah cuilan adonan ke bagian biasa)
| Contoh :3 | 2 | – 2 | 1 | = | 17 | – | 7 | = | 51 | – | 35 | = | 16 | = (16 : 15 = 1 sisa 1) = 1 | 1 |
| 5 | 3 | 5 | 3 | 15 | 15 | 15 | 15 |
Cara 2 : (bilangan bulat + bilangan bundar dan peahan + belahan)
| Contoh :3 | 2 | – 2 | 1 | = 2 – 3 +( | 2 | – | 1 | ) = 1 +( | 6 | – | 5 | ) = 1 | 1 |
| 5 | 3 | 5 | 3 | 15 | 15 | 15 |
3. Penjumlahan dan Pengurangan Pecahan Desimal
Penjumlahan dan pengurangan belahan desimal mampu dilakukan dengan cara bersusun, hal yang perlu diperhatikan yakni nilai tempat bilangan bilangan yang akan dijumlahkan atau dikurangkan harus sempurna. Kesalahan yang sering terjadi ialah penempatan nilai tempat yang tidak benar sehingga hasil pengerjaan hitung juga salah. Dalam pengerjaan hitung penjumlahan dan pengurangan yang diluruskan yakni tanda komanya bukan nilai tempatnya.
| Contoh Penjumlahan: | 2, 36 0, 500 |
+ Contoh Pengurangan | 98,76 5,432 |
– |
| 2, 860 | 93,332 |
4. Penjumlahan dan Pengurangan Pecahan Persen
Untuk penjumlahan dan pengurangan pecahan persen mampu memakai cara bersusun seperti pada penjumlahan dan pengurangan pecahan desimal.
| Contoh Penjumlahan: | 75 % 15% |
+ Contoh Pengurangan | 75% 40% |
– |
| 90% | 35% |
5. Pekalian dan Pembagian
Dalam mengalikan penggalan tidak ada syarat yang mengharuskan penyebutnya harus sama. Perkalian pecahan dilakukan dengan mengalikan penyebut dengan penyebut dan pembilang dengan pembilang, karenanya disederhanakan (jika belum dalam bentuk sederhana).
Secara umum rumus perkalian cuilan yakni sebagai berikut :
| Rumus : | a | x | c | = | a x c |
| b | d | b x d |
| Contoh : | 2 | x | 1 | = | (2 x 1)= 2 |
| 5 | 3 | (5 x 3)=15 |
Khusus untuk pembagian kepingan, salah satu potongan harus dibalik (pembilang menjadi penyebut dan sebaliknya)
Secara umum rumus pembagian serpihan ialah sebagai berikut :
| Rumus : | a | – | c | = | a – d |
| b | d | b – c |
| Contoh : | 4 | – | 1 | = | 4 | – | 3 | = | 1 |
| 5 | 3 | 5 | 1 | 4 |
Terima kasih telah membaca artikel di website kabarpandeglang.com, semoga bisa memberikan informasi yang bermanfaat bagi kamu dan bisa dijadikan referensi. Artikel ini telah dimuat pada kategori pendididkan https://kabarpandeglang.com/topik/pendidikan/, Jangan lupa share ya jika artikelnya bermanfaat. Salam admin ganteng..!!