KABARPANDEGLANG.COM – Lingkaran yakni salah satu bentuk berdiri datar yang banyak dijumpai di sekitar kita. Pengetahuan ihwal bulat dapat banyak diterapkan dalam kehidupan sehari-hari. Misalnya untuk menentukan jarak rumah ke sekolah dengan menghitung banyaknya putaran roda sepeda.
Beberapa istilah yang berafiliasi dengan bangun lingkaran antara lain Diameter, Tembereng, Keliling, Titik pusat, Busur, Juring, Luas, Jari-jari, Tali busur, dan Pi, Bilangan pi (π) yakni salah satu bilangan yang ditemukan sejak zaman dahulu.
Bilangan itu memberikan perbandingan keliling terhadap diameter lingkaran. Meskipun bilangan 22/7 hanya suatu pendekatan, namun hingga saat ini bilangan 22/7 paling sering digunakan di dalam perhitungan bundar
A. Unsur-Unsur Lingkaran
Sebelum mempelajari unsur-unsur lingkaran ingat kembali istilah-istilah terkait lingkaran yang telah dipelajari sebelumnya, yakni titik, garis, ruas garis. Ada tujuh unsur lingkaran meliputi titik sentra, jari-jari, diameter, busur, tali busur, tembereng,, dan juring.
Tujuh unsur bulat mampu dikelompokkan berdasarkan ciri-ciri yang sama dari unsur-unsur bulat tersebut.
- Unsur lingkaran yang berupa titik ada 1, ialah titik sentra.
- Unsur bulat yang berupa ruas garis ada 3, yakni jari-jari, diameter, dan tali busur.
- Unsur bulat yang berupa lengkungan ada 1, yakni busur.
- Unsur lingkaran yang berupa kawasan ada 2, yaitu juring dan tembereng.
| No. | Pernyataan | Benar | Salah | Seharusnya |
|---|---|---|---|---|
| 1 | Titik sentra sempurna berada di tengah lingkaran | √ | – | – |
| 2 | Jarak titik pusat ke semua titik pada lingkaran ialah sama | √ | – | – |
| 3 | Titik sentra pada suatu bundar hanya ada satu | √ | – | – |
| 4 | Panjang jari-jari yakni dua kali lipat dari panjang diameter | – | √ | Panjang jari-jari adalah setengah kali lipat dari panjang diameter |
| 5 | Panjang diameter adalah dua kali lipat dari panjang jari-jari | √ | – | – |
| 6 | Diameter tidak melalui titik sentra | – | √ | Diameter melalui titik pusat |
| 7 | Diameter boleh juga disebut tali busur | √ | – | – |
| 8 | Tali busur boleh juga disebut diameter | – | √ | Tidak semua tali busur ialah diameter |
| 9 | Busur niscaya berupa lengkungan | √ | – | – |
| 10 | Semua titik pada tali busur berjarak sama terhadap titik pusat | √ | – | – |
| 11 | Tembereng dibatasi oleh busur dan tali busur | √ | – | – |
| 12 | Tembereng berupa daerah | √ | – | – |
| 13 | Juring berupa lengkungan | – | √ | Juring berupa tempat |
| 14 | Juring dibatasi oleh 2 jari-jari dan tali busur | √ | – | – |
Berikuy ini unsur-unsur bundar
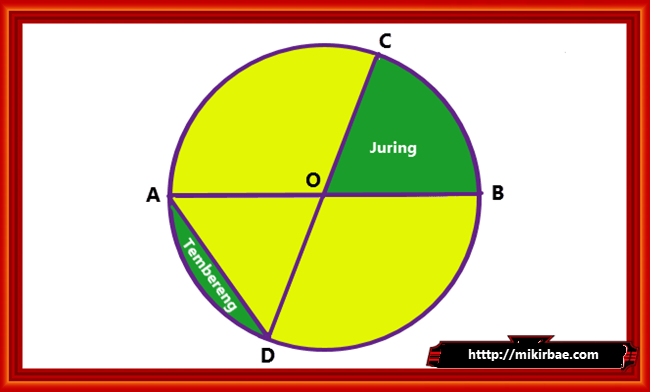
1. Titik Pusat
Titik sentra pada lingkaran merupakan sebuah titik yang terletak sempurna ditengah-tengah lingkaran. Pada gambar di atas titik pusat lingkarannya terletak di huruf O.
2. Jari-jari
Garis OC, OD, OB dan OA pada gambar di atas merupakan jari jari bulat. Jari jari bulat adalah garis yang menghubungkan titik sentra lingkaran dengan titik pada keliling bundar.
3. Diameter
Garis AB dan CD pada gambar diatas di sebut garis tengah atau diameter lingkaran . Diamater yakni panjang garis lurus yang menghubungkan dua titik pada keliling bulat yang melalui titik pusat bulat. Dari hal ini kita dapat mengambil kesimpulan yakni jari-jari bundar memiliki nilai setengah dari diameter atau diameter memiliki nilai dua kali jari-jari. Sehingga bisa di tulis d = 2r.
4. Busur
Garis lengkung AC, CB, BD, AD pada gambar di atas disebut dengan busur bundar. Busur bulat ialah garis lengkung yang menjadi bab dari keliling lingkaran . Busur terbagi menjadi dua yakni busur kecil dan busur besar. Disebut busur kecil kalau panjangnya kurang dari setengah lingkaran dan disebut busur besar bila panjangnya lebih dari setengah lingkaran.
5. Tali Busur
Garis AD yakni pola tali busur lingkaran, tali busur ialah ruas garis lurus yang menghubungkan dua titik pada keliling bulat dan tidak melewati titik sentra bundar. Jika kita ibaratkan maka tali busur umpama tali pada busur panah.
6. Tembereng
Tembereng merupakan daerah yang di dalam bundar yang di batasi oleh tali busur dan busur bundar. Pada gambar di atas tembereng di batasi oleh busur AD dan tali busur AD.
7. Juring
Juring merupakan tempat yang di batasi oleh dua garis jari-jari dan sebuah busur lingkaran yang posisinya diapit oleh dua buah jari-jari tersebut. Pada gambar di atas tempat yang dinamakan juring sebagai contoh ialah kawasan yang di warnai hijau yaitu juring BOC. Juring terbagi menjadi dua yakni juring besar dan juring kecil.
B. Keliling Lingkaran
Keliling lingkaran yaitu bilangan yang menyatakan panjang kurva yang membentuk lingkaran. Rumus keliling lingkaran ialah :
K = π × d atau K = 2 × π × r
Keterangan:
K = Keliling bundar
π = pi (3,14 atau 22/7 )
d = diameter lingkaran
r = jari-jari
C. Luas Lingkaran
Luas bulat ialah luas daerah yang dibatasi oleh lingkaran. Rumus untuk menentukan luas lingkaran ialah :
L = π × r²
Keterangan:
L = Luas bundar
π = bilangan pi (3,14 atau 22/7 )
r = jari-jari
Menemukan Luas Lingkaran
Alat dan bahan:
1. kertas 2 lembar
2. jangka
3. bolpoin
4. penggaris
5. gunting dan cutter
6. lem
Langkah-langkah:
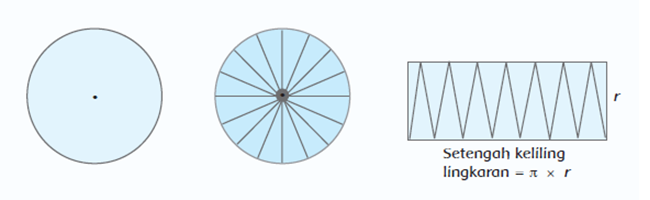
- Buatlah sebuah lingkaran dengan jari-jari 3 cm (misalkan kita beri nama bundar P).
- Potong lingkaran P menjadi 16 kepingan yang sama.
- Ambil satu serpihan kemudian potong menjadi 2 bagian yang sama.
- Susun semua penggalan tadi menjadi bentuk yang ibarat persegi panjang.
Luas lingkaran sama dengan luas susunan potongan juring bundar yang disusun menyerupai bentuk persegi panjang, adalah π × r × r = π × r².
Terima kasih telah membaca artikel di website kabarpandeglang.com, semoga bisa memberikan informasi yang bermanfaat bagi kamu dan bisa dijadikan referensi. Artikel ini telah dimuat pada kategori pendididkan https://kabarpandeglang.com/topik/pendidikan/, Jangan lupa share ya jika artikelnya bermanfaat. Salam admin ganteng..!!